ボラティリティの鬼ことマートン太郎です.Xで上記のようなポストをした以上,ボラティリティの推定の仕方を教えなければなりません.まずはリテラシーレベルとして株価が対数正規分布に従う場合について簡単に手順を説明したいと思います.リテラシーレベルと言っておいて対数正規分布とか何なん,教える気ゼロやろうという声が聞こえてきそうですが,これは雰囲気を伝えるためにやむを得ない用語ですのでお許しください.価格が対数正規分布に従うというのは非常にシンプルで美しい仮定で,ファイナンスの標準理論ではよく採用される仮定になりますので,ある種のベンチマークとしても考えられますし,実際は実務の世界では面倒なのでこの仮定で話がすすめている場合もあります.ある資産価格がどれくらい対数正規分布とズレていて,その場合のボラティリティ推定はどのようになるかなどはアドバンストレベルの記事として書いてみたいというか,すでにあまり説明なしにこのブログではDCC-GARCHモデルやEGARCHモデルを使った分析結果を書いているので,そのあたりをもっとちゃんと説明する機会をもうけようと思っています.
それはさておき,投資家なら誰しも一度は図1のようなリスク・リターン平面をみたことがあるでしょう.縦軸に期待収益率,横軸に収益率の標準偏差(これをファイナンス界隈ではボラティリティ≒リスクとみなします)をとって,各銘柄とかその組み合わせのPFがどの程度リスクをとっていて,リターンが期待きるが可視化してものです.これは単に可視化のためのツールではなく,ある条件の下で,銘柄選択,PF選択というのは,あれこれ複雑に考える必要はなく,ボラティリティと期待収益率と相関で完全に決まり,ボラティリティと期待収益率という2軸の評価に落とし込めるという現代ポートフォリオ理論の舞台になります.
図1:リスク・リターン平面
リスク・リターン平面にはボラティリティと期待収益率というパラメータをプロットするべきものですが,これらは現実的には収益率系列から推定するしかない値です.先に仮定した状況,すなわち,(対数差分)収益率(という確率変数)が独立同一の正規分布に従う場合,期待収益率は収益率系列の標本平均,ボラティリティは収益率系列の標本標準偏差で推定できます.これぐらいならエクセルなどの表計算ソフトでできる範囲内ですので,以下,具体的にやり方を示します.
図2のようにPFの評価額が記録されているとしましょう.これはMyPFの記録です.2020年8月21日から2025年9月2日までのデータ(B1501まで)が入っています.
図2:PFの評価額
次にC列で収益率を計算します.C3に「=LN(B3/B2)」と入力すると2020年8月21日から22日にかけての収益率が計算されます.この計算を繰り返したいのであとはC3のセルをオートフィル機能を使って下に伸ばし,C1501まで収益率を計算したのが図3になります.
図3:収益率
期待収益率とボラティリティを求めます.図4のように適当なセルに(ここではD2とE2)期待収益率はC2からC1501の平均,ボラティリティはC2からC1501の標準偏差を計算します.それぞれ,「=AVERAGE(C2:C1501)*252」と「=STDEV(C2:C1501)*252^0.5」と入力します.期待収益率に252,標準偏差に252の平方根(252の0.5乗)をかけるのは,年率に換算するためで,1年の観測日数が大体252営業日であるためです.なので年によっては252日より多かったり少なかったりしますし,そもそも,観測漏れなどもありますが,このあたりはあまり気にしなくてもいいかと思います.もし,元の観測データが週次データなら1年は大体52週なので52と52の平方根をそれぞれかけます.月次データなら1年12か月なので12と12の平方根をかけます.観測頻度が落ちれば推定の精度は落ちますが,このあたりはデータ観測の手間とのトレードオフになります.
図4:期待収益率とボラティリティ
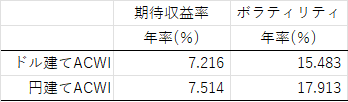
期待収益率やボラティリティを年率に換算するのは,業界の慣習みたいなものです.これによって,他アセットとの比較が可能になります.最初の図1ももちろん年率表示になっています.それではせっかくなのでこの5年分のデータを使って推定した年率の期待収益率とボラティリティを他のPFと比較してみます(正確には図4でちょうどにするなら過去5年はC9からC1501にするべきだが,誤差の範囲内なので,上記の5年と数日のデータで計算した平均と標準偏差を使います).比較対象は円建て配当再投資込みの指数であるeMaxisSlimシリーズからオルカン,SP500,TOPIX,8資産均等型にしました.これらの投信のリターンや標準偏差はYahoo!ファイナンスなどの一般的なサイトでみることができます.原点と各PFのリスク・リターンを結んだ線の傾きは単位リスクあたりのリターン,すなわち,シャープレシオ(リスクフリーレートゼロ版)を表しますので,MyPFが優勝していることがわかります.
図5:MyPFとeMaxisSlimシリーズ
もし,保有しているのがオルカンだけとかSP500だけなら,そのボラティリティはYahoo!ファイナンスをみれば確認できます.ただ,大抵の人は,時にはリスクを下げるために債券やゴールドを入れてみたたり,時には欲張ってレバナスを入れてみたり,個別株を買ってみたり,色々でしょう.アセットアロケーションは日々変化していて,また仮に単一の銘柄しか保有していなくても実はボラティリティは一定ではないということがこれまでの実証研究でわかっています.なので,今この瞬間どれぐらいのリスクを取っているかというのは上記の方法ではわからないということになります.このあたりの事情まで現実のデータの挙動をちゃんと捉えることができるのがGARCH型モデルなどのボラティリティが時間を通じて変動するモデルになりますが,リテラシーレベルを超えるので,このあたりを説明するのはまたの機会にしたいと思います.
そういう意味で,上記でやっているリスク・リターン平面上のボラティリティは過去にとってきたリスクの平均的なレベル,リターンも過去に獲得したリターンの平均です.そして一般的にリスクは再現性があり,リターンに関しては5年程度なら色んな値がでるので,将来のリターンレベルを保証するものではありません.自分がどの程度のリスクをとってきたのかを知らずして,攻めるべきか守るべきか決めることはできない.
彼を知り己を知れば百戦殆からず
ミクロでは企業の決算がどうのこうの,マクロではインフレとか雇用がどうのこうの,ほんとにわかるかどうかよくわからない彼を知る活動は盛んに行われるが,己を知る者は驚くほど少ない.







コメント
コメントを投稿