新NISAオルカン積立のみで億り人になる確率

 　新NISA開始まであと3か月となりました．増税クソメガネとよばれてしまっている岸田さんがやった数少ない減税というか非課税制度の拡充です．僕は信託報酬を半減してくれたオルカン(eMAXIS Slim オールカントリー)で生涯投資枠1800万を5年で埋めたいと思います（といいつつなんか余計なものも買ってしまうかも）．

　巷というかインターネット上では「インデックス投資で億り人とかw」とか「オルカンはもはや安全資産」とか蒙昧無知な言説が蔓延っている気がします．もちろんインデックス投資でも億り人になれますし，オルカンはバリバリのリスク資産です．どの程度のリスクがあるのかとかどの程度の確率で億り人になれるのかとかは割と簡単に計算できます．僕も専門家(笑)としていろんな人に聞かれることが多くなってきました．その時の説明用に各種確率をまとめてここに置いておきたいと思います．

　確率計算するためにモンテカルロシミュレーションを行います．モンテカルロシミュレーションとは乱数を用いて確率モデルから実現値を繰り返し発生させて確率分布を眺める方法です．その際使う確率モデルは幾何ブラウン運動モデルという簡単なものにしておきます．どう簡単かというと収益率分布がどの時点においても独立同一の正規分布になっているという統計学の入門コースで延々繰り返して出てくる正規母集団の場合というやつです．よってまともな高等教育を受けた人なら絶対に理解しているはずです(白目)．最近は高校でも統計をやるみたいなので，ちゃんとした高校生なら普通にわかっていてしかるべき内容です(煽り)．

　それはさておき，実際の株（今回はオルカン）の収益率は正規分布なのでしょうか？実は実際の株の収益率は正規分布とは微妙に違うことが知られています．よって幾何ブラウン運動モデルよりもっと精緻なモデルも考案されているわけですが，今回の目的である月次データを発生させて積立結果をみるという場合においては，幾何ブラウン運動モデルでもより精緻なモデルでも結果にさほど差はでないことが確認できていますので（あまり詳しく書くと研究内容から僕が身バレしてしまうのでやめておきます），ここは思い切って幾何ブラウン運動モデルで押し通りたいと思います．

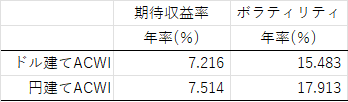
　そうと決まれば，設定しなければいけないことは２つのパラメータのみです．期待収益率とボラティリティです．オルカンの連動指標であるACWI（オールカントリーワールドインデックス配当込み）のデータはMSCIのサイトから誰でも入手できます．1989年1月から2023年6月の34年半のデータを使うと表1のようになります．今回は日本人が円建てで運用することを想定するので期待収益率年率7.514％，ボラティリティ年率17.913％となります．ボラティリティはまあ普通にデカいです．例えば1年だけの投資ならマイナスになる確率は33.74％もあります．こういうのを安全資産とはいいません(長期で運用すればほぼマイナスにならないと言いたいのだと思いますが，それはまた別の話です)．

表1：オルカンの期待収益率とボラティリティ

　それではこの期待収益率とボラティリティを使って50年分(12×50＝600か月分)の月次データを10000通り発生させます．10000とかクレイジ―な回数っぽいですがモデルが簡単なのですぐ終わります．その収益率を使ってオルカンの基準価額系列を10000通り作ってそれぞれの系列で毎月積立を実行して資産額の推移を記録します．積立パターンは月額1万，3万，5万，10万，15万，30万円の6通りとしました．新NISAの1年間の投資上限は360万円，生涯投資枠は1800万円なので，月3万円だと50年間も積立てることになります．

　まず，手始めに少し前に話題になった(ただの野党の煽りでしたが，結果的にいい問題提起になったのかも？)老後2千万円問題をみてみましょう．これは少額投資でも長期間やればほぼ確実に達成できます．月1万円積立の場合は50年間で600万円の元本を投資しているわけですが，9割以上の確率で2千万円以上になりますので，余裕でしょう．

表2：オルカン積立で2千万円を超える確率

　では億り人になれるかについてはどうでしょうか？たとえ月1万積立でも50年600万円の投資で36.76%の確率で億り人になれます．イチローがシーズン262安打したときの打率が3割7分2厘なのでそれと同程度，イチローが打席に立った時，ヒットを期待しない人がいたでしょうか？まあそれはさておき，確率の問題なので億り人になれるか否かということなら，どちらかというとなれるというのは50％以上，なれない側は50％以下とするのが妥当でしょう．月1万はさすがにきついけど，月3万なら45年，月5万なら35年，月10～15万なら30年，月30万なら25年で少なくとも50％以上の確率，すなわち，どちらか言うと億り人になれている方があり得るということになります．

表3：オルカン積立で1億円を超える確率

　金融資産1億円以上というのは，富裕層の定義として野村総研の調査で用いられるものです．長期で達成できるといわれても，長い時間を経ると株価が上がったということなので，当然物価も上がっていて1億円持っていても富裕層とは言えない状況になっている可能性大です．　なので野村総研の定義で超富裕層とされる5億円以上になる確率をみてみましょう．元本が1800万円なのでさすがにきびしいですが，月15万や30万なら50年後に50％を超える確率で超富裕層になれます．

表4：オルカン積立で5億円を超える確率

　このようにオルカンの長期積立はほぼ勝ち確のヌルゲーで，問題はちゃんと続けられるかのみとなります．資産がマイナスになるのは誰しも気分が悪いものです．オルカンは普通に株ですし，リスク資産ですし，ボラティリティがデカいです．そのデカいボラティリティを受け入れるからこそ年率7.514%のリターンを受け取れるわけです．積立初期はマイナスを受け入れなければなりません．5年後の元本割れ確率は19.55％です．15年で一桁パーセント，20年で5％以下になります．

表5：オルカン積立で元本割れする確率

　確率を理解せずに「未来のことはわからないから考えても仕方ない」という人が割といます．何が「わからない」のかを考えないといけません．確率分布がわかっても起こる結果はわかりません．サイコロ投げで出る目はわかりません，というか，予想しても無駄というものです．しかし，1~6までの目が1/6の確率で出るという確率分布は完全に分かります．確率分布(=確率モデル)がわかれば，確率計算に持っていけます．あとは，というか最初から最後まで問題になるのは，仮定した確率モデルが妥当か否かです．

　上述したように，データへの当てはまりの良さという点では幾何ブラウン運動よりもっと精緻なモデルを使ったほうがいいです．しかし，繰り返しになりますが，今回の目的である積立投資のパフォーマンスの確率計算では幾何ブラウン運動で十分です．

　またモデルの仮定で7.514％の期待収益率は楽観的過ぎるから，もう少し低めの5％でやってみましたみたいな設定をする素人もいるかと思います．もちろん次の10年，20年，．．．，50年で7.514％より全然低い収益率になる可能性もあります．その場合の基準価額系列はちゃんと10000系列に含まれていて，つまり，確率モデルには組み込まれているので，余計なことをしてはいけません．まあ，ピケティの「21世紀の資本」のr(資本収益率)が5％程度ということですので，全世界のあらゆる資産の資本主義の時代の平均が5％だったら，債券とかも入っているわけなんで，リスク(ボラティティ)が相対的に高い全世界株の期待収益率が7.5％なのは普通なんじゃないかと思います．